Exercícios Resolvidos de Área entre Curvas

Ver Teoria

Exercício 328 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

UFPB – Cálculo 2 – Listas Prof. Otoniel Nogueira – Lista 04 – Questão 1

Calcule a área da região situada entre o eixo e o gráfico da função com no intervalo

Passo 1

Oi, tudo bem?

Vamos calcular essa área aqui

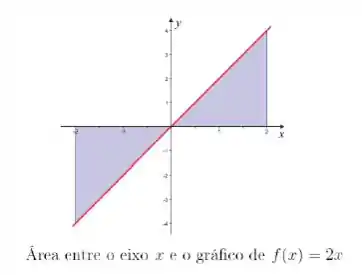
Quando integramos procuramos a função que está mais em cima e a que está mais embaixo. No nosso caso no as funções trocam de posição!

À esquerda da origem a função que está mais acima é o eixo (equação de ) e à direita quem está mais acima é a função . Como queremos a região que está entre , então vmaos precisar dividir nossa região em duas.

Então aqui atenção: vamos começar dividindo nossa região em duas partes e depois é partiu integrar!

Bora começar?

Passo 2

Agora vamos começar dividindo nossa região em duas partes: de até e depois até . Sempre fazendo dentro da integral “a função mais em cima menos a função mais embaixo”