UFU, Sem Campus, Cálculo 1, Listas de C1 - Profº Rafael Rossato - Integrais com coordenadas polares, Questão 5
Calcule a área da região situada no 1º quadrante, limitada acima pela curva (coordenadas cartesianas) e abaixo por (coordenadas polares), com .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para calcularmos a área no 1º quadrante limitada por duas curvas:
E
Para isso, devemos primeiramente passar a primeira equação para coordenadas polares.
Em seguida... devemos saber que a área de uma curva polar em um intervalo , é dada por:
Sabendo disso, devemos pegar curva da maior área e subtrair pela curva de menor área!!
E aí? Bora lá aplicar?
😉
Passo 2
Utilizando as relações entre coordenadas cartesianas e polares, podemos definir a curva para a seguinte curva em coordenadas polares:
Assim, desenhando a curva no plano polar, temos:
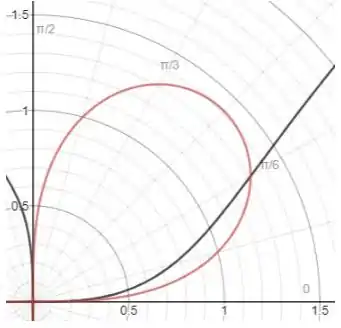
Agora, para descobrirmos o intervalo de integração, devemos igualar nossas duas equações:
De cara, vemos que é uma solução válida. Agora vamos descobrir outro valor:
Logo, temos o intervalo .
Passo 3
Nesse sentido, temos:
Resolvendo a integral, temos:
Entendeu direitinho? Responde aee ;)
