UFPB, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - Lista de Exercícios 2, Questão 2
Calcule a área sob o gráfico de entre e .
Passo 1
Eaee!!! Belezinha? Bom...a questão nos dá uma expressão e nos pede para calcular a área no intervalo de a . Basicamente, queremos descobrir o valor da seguinte integral:
Em outras palavras, queremos encontrar a área sob a seguinte curva:
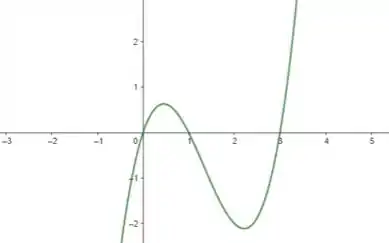
Para isso, pela curva apresentada, basta dividirmos a integral acima em três intervalos:
- De a ;
- De a ;
- De a .
Obs: No intervalo de a a integral será negativa.
Não entendeu? Então bora junto 😉
Passo 2
Bom... dessa forma, desmembrando a integral e resolvendo, temos:
Obs:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x