Calcule a integral
onde é um sólido com fronteira dada por , , e .
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nessa questão temos uma integral tripla limitada por uma região que é descrita por um elipsoide dado por em que , e são maiores que .
O objetivo dessa questão é calcular a integral .
Compreendeu? Como podemos começar nosso probleminha?
Como dito anteriormente, a equação que descreve a região é um elipsoide. Quando temos uma integral tripla onde a região de integração é um elipsoide temos que fazer uma mudança de variável pra facilitar o cálculo da integral.
Quando fazemos uma mudança de variável, precisamos aplicar tipo um fator de correção, no caso, um jacobiano.
O jacobiano é obtido pelo determinante
Bora começar nossos cálculos? 😁
Passo 2
Primeiro, vamos fazer uma análise da região
Seria muito bacana se a gente pudesse simplificar essa equação, não é? E é exatamente isso que vamos fazer!
E se a gente escrever esse elipsoide como uma esfera? Integrais triplas sob coordenadas esféricas a gente sabe fazer, não é? Então fazemos a transformação
Com isso, tiramos que
Temos nossa nova região de integração e a relação entre as coordenadas antigas e as novas coordenadas.
Assim podemos calcular o jacobiano substituindo , e por cada uma de relações com , e .
Por derivação polinomial
já os demais termos da matriz é já que a variável de derivação não está presente na função de derivada, ou seja, na pratica é como se derivássemos uma constante e como sabemos, a derivada de uma constante é .
Com isso, nossa matriz jacobiana será
Logo
Tranquilo até aqui? 👀
Passo 3
Dessa forma podemos escrever nossa integral, como
Mas agora como nosso é uma esfera, podemos seguir os cálculos convertendo nossa integral tripla em uma integral esférica.
Como , vemos que o raio da nossa esfera é , já que as variáveis estão igualadas a .
Lembra das relações , e que fazemos quando convertemos as coordenadas de uma função por coordenadas esféricas?
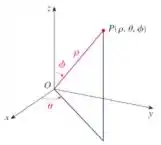
Como nosso é uma esfera completa, os intervalos de , e que descrevem uma esfera completa é
Integrando por integral esférica, lembrando que o jacobiano dessa transformação é
Como são constantes, podem sair da integral
Interessante, não é? 😁
Passo 4
Para calcular a integral, podemos usar um método para dividir as tarefas onde calculamos a integral da sua variável separadamente e multiplicamos os resultados no fim.
Não entendeu nada, não é? Veja só, o que podemos fazer é
Ou seja
Melhorou, né?
Agora calculamos as integrais.
Pelo teorema fundamental do cálculo, sabemos que a integral do é igual a , logo
Aplicando os limites de integração
Sabemos também que a integral de uma constante é a própria constante multiplicada pela constante de integração
Aplicando os limites de integração
Por fim, por integração polinomial, a integral de será
Aplicando os limites de integração
Interessante esse método, não é? Nos ajuda na organização da resolução.
Passo 5
Por fim, a gente multiplica os resultados e substitui na integral maior
Ou seja, a integral que queríamos lá no início resulta em
Ou seja, esse é o volume de um elipsoide!
É isso! Essa resolução te ajudou? Responde Aí! ✌
