USP– Cálculo 1 – Lista 2 – Questão 3.6
Calcule , interpretando-a como uma área
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou descomplicar para você! O problema deu essa região
E pediu para desenharmos a região e calcular a área!
Mas como resolver isso?
Precisamos fazer um esboço da região que pretendemos achar! Temos uma reta que corta o quadrante em duas partes, bem na metade no ângulo de . E temos a parte de cima de uma circunferência
então saca só como fica nossa região:
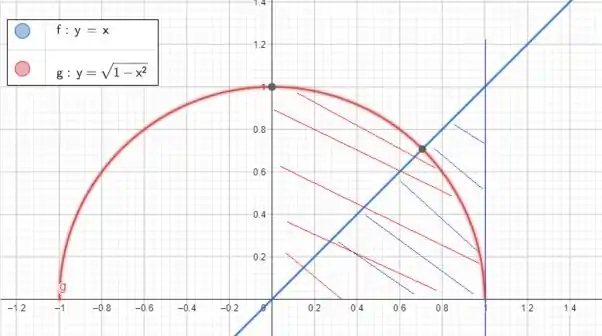
As regiões hachuradas é nossa integral!
Beleza?
Nossa missão é calcular e de preferência sem integrar!
É isso! Bora lá?
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Vamos começar analisando a figura com cuidado! Se tivéssemos apenas a circunferência teríamos um quarto de circunferência (em vermelho), mas tamos também a área do retângulo (em azul)
Beleza?
A área do círculo é
E nosso raio é !
Agora é só calcular!
Passo 3
Queremos apenas do círculo
Agora queremos a área do triângulo de lados
E a integral fica
Show! E é isso pessoal! Espero ter ajudado!