UnB, Sem Campus, Cálculo 2, P1 - 2008.2, Questão 2a
Considera-se a área entre a curva e o eixo para .
a) Determinar a medida de e as coordenadas do centroide .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar o valor da área que é medida verticalmente entre a curva e o eixo e horizontalmente entre e . Além disso, nós vamos precisar determinar as coordenadas do centroide dessa área. Mas vamos por partes.
Para determinar a área , vamos dar uma olhadinha no gráfico:
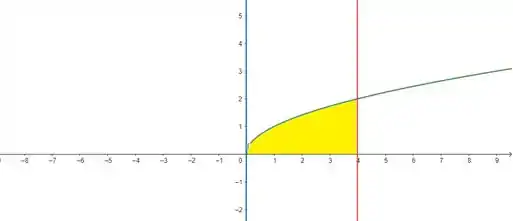
Repare que em azul nós temos a reta , em vermelho a reta e em verde a curva . Nossa área é essa aí em amarelo, para calculá-la nós vamos precisar resolver a integral:
Já o centroide, ou centro de massa da área, tem suas coordenadas dadas por:
Vamos lá!
Passo 2
Vamos começar calculando a área através da integral:
Vamos colocar a raiz em forma de potência:
Assim, usando a regrinha da potência (), temos:
Fazendo a divisão de frações:
Aplicando os intervalos de integração:
E temos nossa área:
Passo 3
Agora vamos calcular as coordenadas do centroide, dadas por:
Começando pela coordenada :
Usando e a área que calculamos no passo anterior, , temos:
Somando os expoentes de e :
Usando a regrinha da potência para integrar:
Aplicando os intervalos de integração:
Assim, temos:
Passo 4
Calculando agora a coordenada , temos:
Substituindo e :
Elevando a raiz ao quadrado e colocando as constantes fora da integral, temos:
Integrando:
Aplicando os intervalos de integração:
Então, nossas coordenadas do centroide são .
Valeu, galera! Até a próxima! 😉