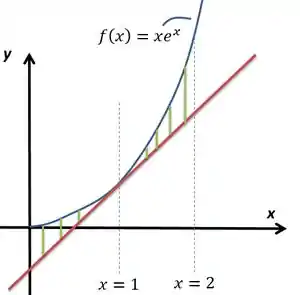
Considere definida por e a reta tangente ao gráfico da em . Calcule a área da região destacada na figura abaixo:
Passo 1
Para essa área ser calculada a gente precisa dos limites de integração, da disposição das funções entre as quais calculamos a área e da equação de cada uma das funções.
Em primeiro lugar, os limites de integração estão bem claros no enunciado e no desenho, temos o variando de até .
Além disso, sabemos que está sempre mais alta que a reta para , essa é a disposição gráfica delas nesse intervalo.
Agora, não conhecemos a equação própria da reta . Vamos desenvolvê-la e então poderemos calcular a seguinte área:
Passo 2
Modelando por uma equação nós podemos achar como sendo a derivada da função no ponto de tangência, . Primeiro vamos derivar em função de :
Para descobrir podemos aplicar a reta modelada no ponto dado por , ao qual ela pertence:
Enfim, a reta será .
Passo 3
Agora é só fazer a integral para descobrir a área:
A única integral mais chata é a do primeiro termo, que podemos fazer por Partes:
As outras primitivas saem pela integral normal de polinômios:
Essa é a área que nos interessa!