UFSC – Cálculo C – P1 – Questão 2 (ADAPTADO) – Parte II
Considere a área da região de intersecção às curvas e . Esboce a região
Parte II) Calcule a área da região de intersecção
Passo 1
E aí pessoal, tudo bem? O problema nos deu essas duas curvas
Por simplicidade dividimos essa questão em duas partes. Na parte (i) fizemos o esboço da região. Agora na parte (ii) vamos calcular o valor da área!
#partiu calcular essa área então!
Na parte I nós fizemos o esboço dessa região, encontramos isso aqui
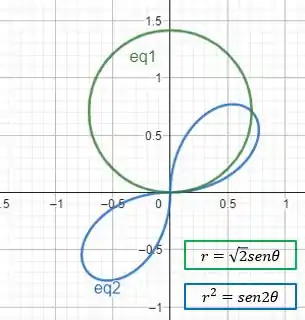
o ponto onde as curvas se encontram fora da origem é em
então precisamos dividir a região a ser calculada em duas
- Região I
- Região II
- Começando pela Região
Pois elas alternam quem está mais “por fora”. Lembrando que o diferencial de área em coordenadas polares é
Vamos dividir essa região em duas
E integrar!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
A integral fica
Tranquilo até aqui?
Vamos começar resolvendo a integral em
Tranquilo? Lembrando que , podemos calcular por fim a parte em
Continuando temos
E por fim, aplicando nos limites de integração e simplificando
E é isso! Vamos guardar esse resultado!
Passo 2
Agora a região :
A integral fica
As integrais são as mesmas, mudando apenas os limites de integração, então vamos reciclar alguns resultados. Começando em
E agora em
Integrando e aplicando nos limites
Passo 3
Por fim vamos reunir os resultados!
Espero ter ajudado! Vamos para a próxima?