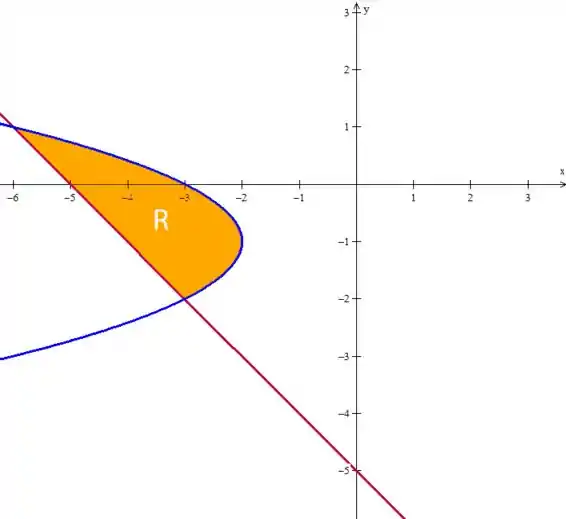
Considere as curvas e .
- Esboce as curvas acima em um mesmo plano cartesiano exibindo os pontos de intersecção com suas abscissas e ordenadas.
- Exiba uma ou mais integrais que determinem a área da região delimitada por estas curvas.
- Calcule a área desta região.
Passo 1
Vamos primeiro esboçar cada região. Isolando :
Trançando a reta:
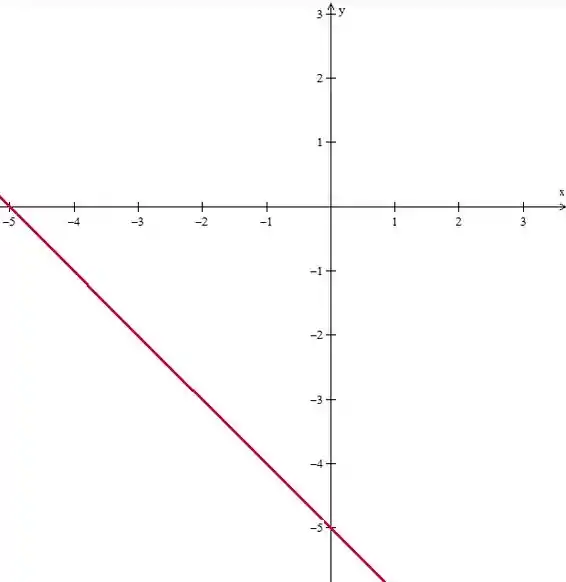
Para a outra curva, podemos considerar como uma função de , onde:
Que é a parábola virada: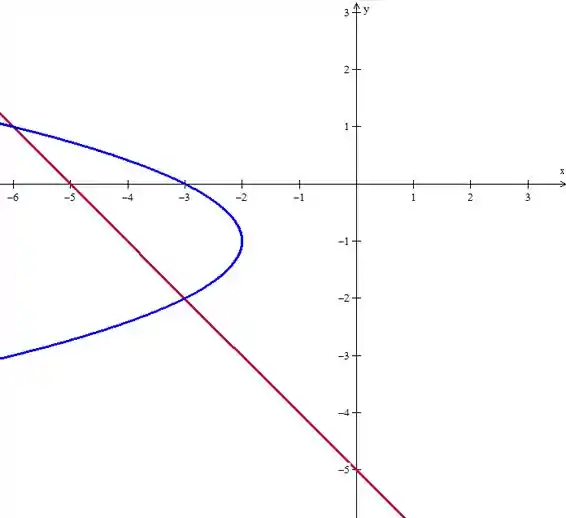 
Da própria figura, vemos que as curvas se tocam em e .
Passo 2
Vamos agora determinar a área da região , que está entre as duas curvas:
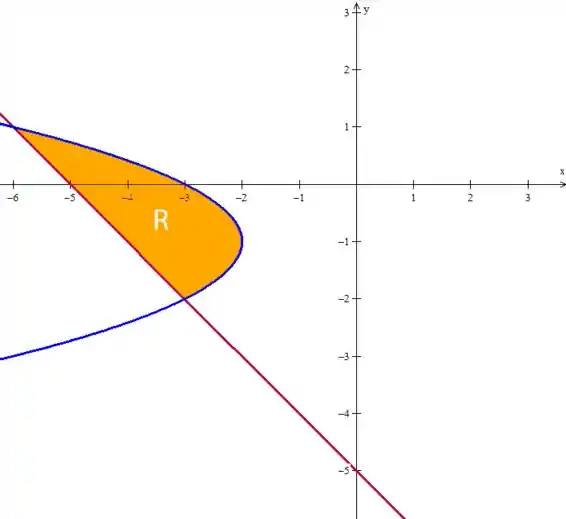
Como a parábola é difícil de isolar, vamos integrar em relação a mesmo. Pelo gráfico, temos que o ocorre em e o em . Esse será nosso intervalo de integração.
A curva superior é aquela que está mais a direita e será, portanto a parábola.
E a curva inferior é a reta, que em função de será:
Assim sendo, a área será:
Passo 3
Calculando:
Sendo u.a. unidade de área.
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x