Considere a integral
(1) Desenhe a região de integração. Justifique.
(2) Trocando a ordem de integração, calcule a integral .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nessa questão temos uma integral onde pelos limites de integração, podemos identificar a região de integração como a região limitada pelas curvas , , e .
A função de integração da nossa integral é dada por .
No item 1) temos que desenhar a região de integração.
Já no item 2) temos que inverter a ordem de integração e obter o valor de .
Mas como podemos fazer isso? 👀
Analisando os limites de integração de , podemos definir as curvas que limitam a região de integração.
Já com a região de integração desenhada, vamos converter nossa integral do tipo 1, onde varia entre um intervalo numérico e entre duas funções, para uma integral do tipo 2, onde varia de um intervalo numérico e entre duas funções.
Tudo Pronto? Bebe uma água e bora começar! 😎
Passo 2
Passo 3
Passo 4
Plotando as curvas , , e , vamos obter a seguinte região.
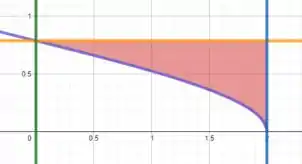
Com isso, já completamos o item 1)
Agora o desafio é escrever variando entre duas funções.
Pra isso, analisando o limite máximo da região de integração vermelha, vemos que a reta azul () vai ser o limite superior da integral .
Agora vemos que o limite inferior é dado pela curva roxa ().
Como podemos fazer para escrever a mesma curva em função de ?
Podemos escrever como , ou seja
Se multiplicarmos os dois lados por , podemos isolar o em um lado da equação.
Multiplicando os dois lados por , vamos eliminar o
Isolando em um lado da equação, temos
Com isso, descobrimos que o intervalo de integração de é
Compreendeu? 🤩
Passo 5
Agora descrevemos o intervalo de integração em como um intervalo numérico. Analisando a região, vemos que o valor máximo de é quando a região está na reta laranja () e o menor valor é na intersecção entre as curvas roxa e azul.
Bora ver que ponto é esse
Igualando as duas equações, temos
Ou seja, quando !
Dessa forma, o intervalo de integração para será
Com isso, nossa integral terá a seguinte cara
Podemos começar a calcular nossa integral
Calculando a integral de , temos
Substituindo por e aplicando o método da substituição.
Desfracionando a função de integração e calculando pelo método da integração polinomial
Voltando para
Tranquilo até aqui? 😉😉
Passo 6
Aplicando os limites de integração
Agora com base nesse resultado, integramos com relação a
Como as propriedades das integrais nos permite, podemos fazer o seguinte
A integral de uma constante é a própria constante multiplicada pela variável de integração
Aplicando os limites de integração
Está acompanhando?
Passo 7
Já a outra integral parece muito complicada, não é?
Mas se lembrarmos das identidades trigonométricas do , podemos lembrar que
Com isso, simplificamos nossa integral para
Como sabemos, a integral do é o , ou seja
Aplicando os limites de integração.
Com isso, vemos que
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
