Área Entre Curvas
Considere a região delimitada pelas curvas e
Esboce a região .
Calcule a área da região .
Passo 1
Para esboçar vamos primeiro reparar que um gráfico é , que vem de para e depois explode para , e o outro é , que tem raízes em e e tem concavidade para baixo, já que o termo que multiplica o é negativo. Vamos analisar a interseção dos gráficos:
Conluímos, assim, que a região será dividida em dois pedaços, um de a e outro de até . Vamos ao esboço:
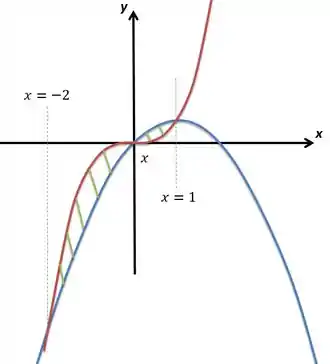
A região está pintada de verde.
Passo 2
Para calcular a área devemos montar uma integral com a diferença entre a função mais alta para a mais baixa. No intervalo a maior é a vermelha , em a mais alta é a azul :
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x