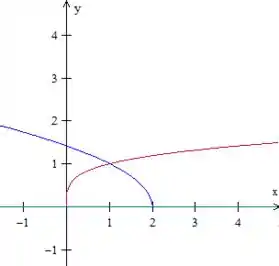
Considere a região delimitada pelas curvas e ,
Esboce a região .
Determine uma integral ou soma de integrais em que represente a área desta região.
Determine uma integral ou soma de integrais em que represente a área desta região
Calcule a área da região .
Passo 1
Vamos um por um: imaginando que seria uma parábola em pé, seria o quadrado dessa parábola, ou seja, uma parábola mais esticada, trocando os valores de e , o vai ser como uma parábola deitada.
O vai ser uma meia-parábola, crescendo para o lado negativo de , com sua raiz em . Além disso, o será uma reta horizontal em cima do eixo , onde vale .
Juntando tudo, ficamos assim, com essa região de até :
c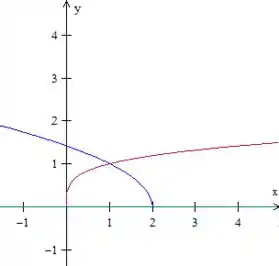
Passo 2
Olhando o gráfico, a gente vê que podemos achar essa área como a integral de de até e de de até , dado que o ponto de encontro dos gráficos é :
Desconsiderando valores complexos e dado que nossa região só tem , o único valor satisfatório é , que gera .
Logo,
Passo 3
Olhando o gráfico, a gente vê que podemos achar essa área como a integral de
Menos de até , dado que o ponto de encontro dos gráficos é , como já calculado:
Logo,
Passo 4
Resolvendo a segunda integral:
Resposta