UTFPR, Sem Campus, Cálculo Diferencial e Integral 1, Provas - Profª Lilian Brambila - P3 2023.1, Questão 5
Considere a região R delimitada pelas curvas y = x², y = 0 e x = 1. Faça um esboço da região R e encontre o volume do sólido obtido pela rotação da região R ao redor de x = 2.
Passo 1
Beleza meu consagrado? Espero que sim, aqui é o Yuri e vamos nessa para mais uma resolução.
Hoje vamos ter que encontrar o volume de um sólido de revolução, então bora.
Utilizando do nosso amigo GeoGebra, iremos gerar o esboço da região R. Ela está acima do nosso eixo x, abaixo de e limitada por . Ela irá girar em relação ao eixo , e isso é importante demais.
O volume de uma região rotacionando em torno de uma reta fora da origem, que é o nosso caso pois a nossa região está rotacionando fora da origem, o volume é dado pela fórmula
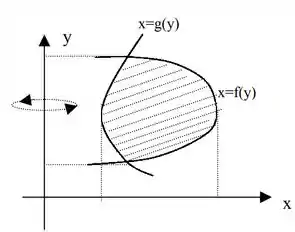
No nosso caso, estaremos rotacionando nossa região ao redor da reta .
Passo 2
Às vezes, o sólido de revolução é gerado em torno de um eixo externo que pode ser paralelo a "x" ou a "y". O método dos anéis circulares, pode ser aplicado, desde que se identifique o raio do giro.
Então temos que de x = 1 até x = 2 temos um raio interno de . Já o raio mais externo é dado por pois ele varia em conjunto com a função .
Passo 3
Calculando agora o nosso volume