Considere a região plana
a) Esboce abaixo a região .
b) Escreva a área da região através de uma soma de integrais na variável . Atenção: Neste item não é necessário calcular as integrais.
Passo 1
a) Fala aí! Tá bem? Para esboçar essa região, vamos ter que interpretar cada uma dessas inequações.
Começando por
Se ali fosse um sinal de igual, teríamos
E isso é a equação de uma circunferência de raio e centro . Para descobrir isso, é só comparar essa equação com a equação geral da circunferência:
Mas como temos um sinal de desigualdade, a gente está olhando para uma região. Ou a região dentro da circunferência ou fora. Para descobrir, a gente pode testar se o centro da circunferência, que é um ponto dentro dela, satisfaz essa inequação ou não:
A gente sabe que zero não é maior que 4, então esse ponto que está dentro da circunferência não satisfaz a nossa inequação. Sendo assim, a nossa inequação descreve a região fora do círculo. Aí marcando essa região:
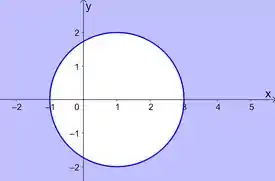
Passo 2
Vamos olhar agora
Essa parte
Diz que precisa ser positivo. Ou seja, a gente está olhando para a parte acima do eixo . Agora vamos analisar a outra parte:
Isso significa que está limitado por cima por uma curva de expressão . Como só um dos termos está ao quadrado, a gente vê que isso é uma parábola. E ela está virada para cima.
Para esboçar ela, a gente pode achar 3 pontos dela, sendo um deles o seu ponto mínimo. Para achar esse ponto, a gente pode derivar a equação da parábola e igualar a zero, isso vai nos dá seu único ponto crítico (o mínimo).
Então o ponto de mínimo é . Aqui também poderia usar aquela fórmulinha de mínimo de uma parábola, Daria a mesma coisa, tá?
Se a gente substituir e , achamos os outros 2 pontos: e . Aí esboçando essa parábola, e a região limitada por cima por ela e por baixo pelo eixo , encontramos:
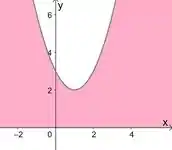
Passo 3
Cara, agora a gente faz a interseção entre essas duas regiões. E como ele diz que:
A gente só marca a região da interseção que estiver também dentro desse intervalo. Fazendo isso, achamos :
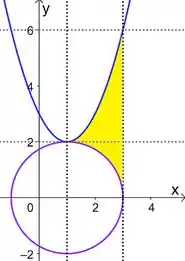
Passo 4
b) Agora a gente precisa descrever essa região como uma soma de integrais em . A gente vai usar essa fórmulinha:
O que ela quer dizer? é a nossa região, é o intervalo de onde essa região está, é a função que limita a região pela direita, e , a função que limita pela esquerda.
No eixo , nossa região está entre a interseção de e a parábola, que é e a circunferência, que é . Ou seja, está no intervalo
Mas repara ali no nosso gráfico que no intervalo , nossa região está entre e a circunferência. Já no intervalo de , nossa região está entre outras funções: e a parábola.
Por isso, a gente vai precisar separar isso em duas integrais! Uma para cada um desses intervalos:
Passo 5
Olhando para o intervalo
A gente vê que a função que limita nossa região pela direita é a reta . Aí a gente pode escrever
E a função que limita nossa região pela esquerda é a circunferência de equação . A gente precisa de uma expressão na forma , então vamos isolar :
Como é a parte da circunferência onde (pelo gráfico), a gente quer a parte positiva dessa raiz. Dizemos então, que a função que limita nossa região pela esquerda é
Aí a nossa integral para esse intervalo fica:
Passo 6
Olhando para o intervalo
A gente vê que a função que limita nossa região pela direita é também a reta . Aí a gente pode escrever
E a função que limita nossa região pela esquerda é a parábola de equação . A gente precisa de uma expressão na forma , então vamos isolar :
Como é a parte da curva onde (pelo gráfico), a gente quer a parte positiva dessa raiz. Dizemos então, que a função que limita nossa região pela esquerda é
Aí a nossa integral para esse intervalo fica:
Passo 7
Com isso, nossa região pode ser descrita pela soma:
Ufa! Deu tudo certo!
Resposta
a) 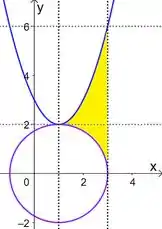
b)