UFF, Sem Campus, Cálculo IIA, Avaliações a Distância (AD) - AD1 - 2023.1, Questão 4b
Considere a região plana limitada pela curva , pelo eixo e pelas retas e .
Use o item anterior para obter por meio das áreas ali calculadas.
Passo 1
Fala aí galera, tudo na paz?
Então, nessa questão temos uma região que é limitada pelas curvas:
Usando essas informações, esboçamos a região :
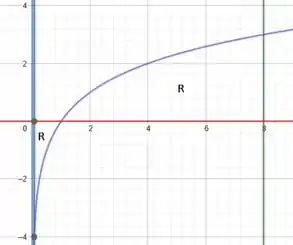
Além disso, usando esse esboço também calculamos a área da região , como sendo:
onde:
E:
Massa!
Nesse item precisamos usar esses resultados encontrados anteriormente para calcular:
O grande ponto aqui é conseguirmos identificar uma área associada à essa integral, beleza?
Então vamo nessa!
Passo 2
Bom, vamos tentar identificar qual região tem área que corresponde à seguinte integral:
Temos que a curva está entre o e o eixo . Isso no intervalo de até .
Isso é exatamente a nossa região , com uma única diferença!
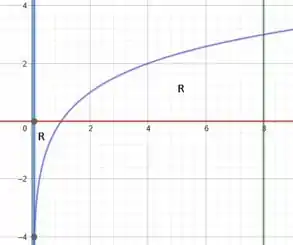
Nessa integral estamos ignorando a “área negativa” no trecho de até (raiz da curva ). Ou seja, quando fazemos a integral:
Estamos fazendo:
Vamos então calcular essa área usando os resultados do item anterior, e comentado no passo :
Resolvendo as integrais:
Portanto:
É isso pessoal, terminamos 😊
Obrigado pela atenção!!