Considere a região plana limitada pelas curvas , e :
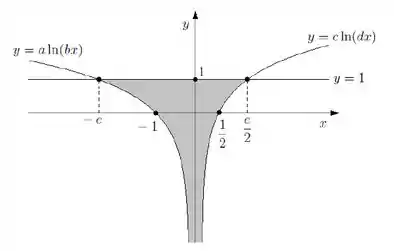
- Utilizando as informações fornecidas no esboço acima, determine o valor das constantes , , , .
- Escreva a área de como uma integral ou uma soma de integrais na variável
- Escreva a área de como uma integral ou uma soma de integrais na variável
- Calcule a área de pelo método que preferir
Passo 1
Partiu começar então. A primeira coisa a se fazer é trocar essas letras todas , , , por alguns números. Vamos começar pela reta . Da propriedade dos logarítimos, veja que:
Sendo assim:
Bem, nessa curva, se olharmos pro esboço, vemos que acontece quando . Sendo assim:
Um outro ponto que o esboço dá é o o ponto . Substituindo esses valores:
Então fechamos a primeira curva, vamos pra próxima. Só repetir as mesmas ideias:
Como ocorre pra segunda curva quando , vamos ter:
E o outro ponto, do esboço, , pode ser usado:
Fechamos então os valores das quatro letras:
Passo 2
Do jeito que a função está desenhada, fica um pouco complicado escrever a área em função de . Porque? Bem, se as áreas são escritas assim:
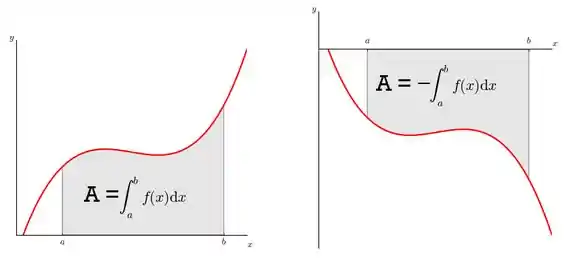
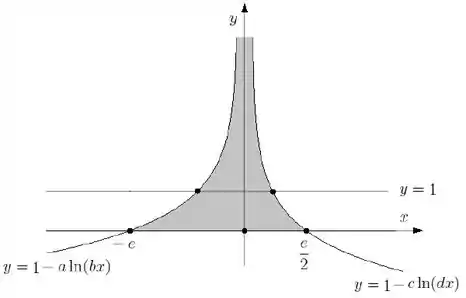
Então, no esboço do enunciado, que temos:
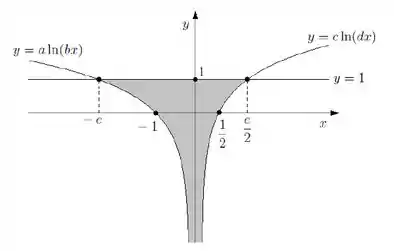
Não rola fazer a integral das duas curvas , uma vez que a área delimitada não é a abaixo da curva e sim a acima. Mas olha só a sagacidade: e se espelhássemos a imagem acima em relação ao eixo ? Aí estaríamos multiplicando todas as curvas por e ficaríamos com:
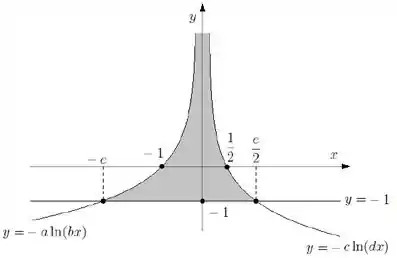
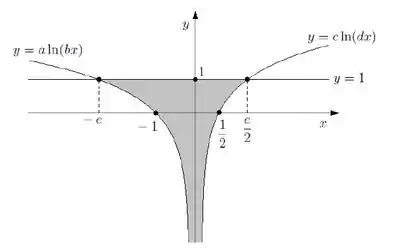
Ok, agora já ficou um pouco melhor. Dá uma olhada que agora a área a se calcular é uma região abaixo da curva. Mas ainda não dá pra calcular a integral direto. Agora, se somarmos a todas as curvas, vamos ter:
Opa agora sim! A integral vai ficar então:
Passo 3
Pra escrever a área toda em função de , a primeira coisa a se fazer é inverter a equação odas curvas. Saca só:
O mesmo vale pra outra curva:
Ta, mas e daí? Veja bem, como é uma função de , temos que ver como que varia na região para achar os limites de integração! E veja bem o esboço original:
Não é que a região está delimitada entre os valores e ? Então taí, são exatamente esses os limites de integração. Como quando a gente inverte uma função é como se tivéssemos trocando os eixos e de lugar, girando o gráfico pra direita e espelhando em relação à horizontal, vamos ter o seguinte esboço:
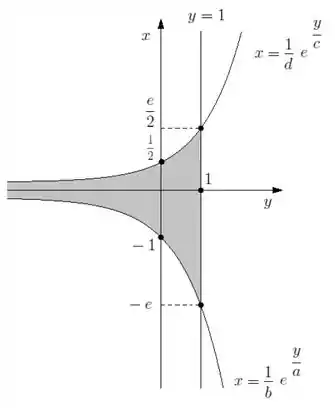
Agora sim fica mais claro de ver a expressão da área, não é mesmo? Vamos ter então que:
Passo 4
Partiu então fechar a questão com chave de ouro calculando a área. Como integrais de são mais chatinhas de se fazer, e a gente pode escolher o método, vamos calcular através da fórmula achada na letra anterior:
A integral de é ninguém menos que ele mesmo! Sendo assim:
Como , podemos reescrever o limite da seguinte forma:
E cortando o termo , que tende à , vamos ter: