UTFPR, Sem Campus, Cálculo Diferencial e Integral 1, Provas - Profª Lilian Brambila - P3 2023.1, Questão 3
Considere o triângulo de vértices (0, 4), (2, −2) e (4, 0). Faça um esboço do triângulo e utilize integral para calcular sua área.
Passo 1
Olá, aqui queremos calcular uma área com uso de integrais.
Então precisamos lembrar que a área de uma região é a integral da curva de cima menos a curva de baixo. Ou, se vamos derivar em y, a integral da curva da direita, menos a da curva da esquerda. Calma que você vai entender isso!
Para nos ajudar com o esboço iremos utilizar o GeoGebra.
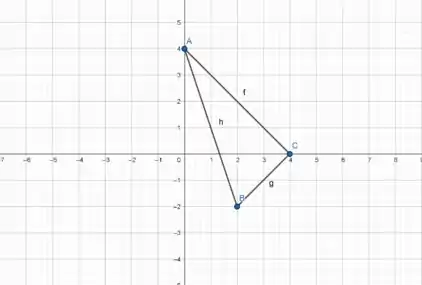
Já adianto que aqui a gente vai precisar de duas regiões, porque não temos como definir toda a região apenas entre 2 curvas. Ou separamos em x=2 ou separamos em y=0. Os 2 casos dão certo igual.
Passo 2
Para que possamos calcular a nossa área, será necessário encontrar as funções .
Para encontrarmos essa nossa equação, poderemos utilizar de duas formulas:
Para AC
Para AB
Para CB
Podemos agora calcular nossa área? Sim e não, a forma que a nossa figura está dificulta um pouco calcular nossa área por meio de integração, então iremos dividir a nossa figura em duas para facilitar nossas vidas.
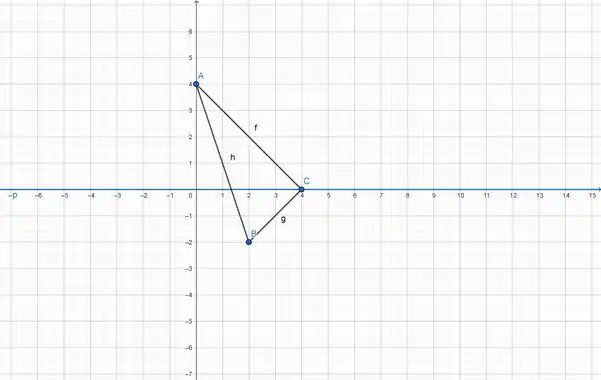
Passo 3
Para resolver iremos dividir em relação a . Para calcularmos a área de utilizando a integral, o que iremos fazer é integrar a função de cima, a mais superior, menos a de baixo. Veja a seguir para ver se ficou claro.
Calculando a área do triangulo superior, teremos.
Para o triangulo inferior,
A área total é entao a soma das nossas duas áreas,