UNICAMP – Cálculo 1 – Professor Ricardo Martins – Lista de Integrais
10.5 Decida se cada afirmação é verdadeira ou falsa. Justifique as verdadeiras e corrija adequadamente as falsas.
a) A integral
Calcula a área da região limitada pelo gráfico de e o eixo , com .
Passo 1
Falaaa... tudo bem??
Nessa questão está dizendo que a integral é utilizada para calcular a área da região delimitada pelo gráfico de e o eixo ou seja, , no intervalo de e .
Pra isso vamos lembrar que quando usamos integral pra calcular a área no gráfico fazemos a integral da função que estiver em cima menos a função que estiver embaixo.
Passo 2
Vamos fazer um esboço dessa função pra analisar:
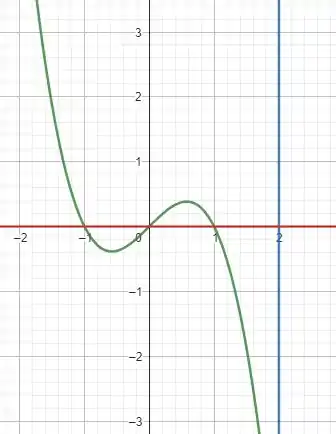
Temos a função em verde e em vermelho.
Se fosse entre e daria certinho, né? Porque nesse intervalo a função está em cima, maaaas de 1 até 2, a função que está em cima é .
Portanto, a afirmação é falsa.
Resposta
Falsa