Desenhe o conjunto abaixo e calcule a área:
m) é o conjunto do plano limitado pelas retas , e pelos gráficos de e .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para determinarmos a área e desenharmos a curva em que de forma que está contido no intervalo .
Para podermos resolver isso, devemos encontrar o resultado da integral de no intervalo dado de .
E, com o auxílio de um software, plotamos a curva e conferimos se o resultado da área bate com a calculada.
Não entendeu? Então bora junto 😉
Passo 2
Bom... dessa forma, temos a seguinte integral (onde é a área):
Passo 3
Dessa forma, plotando a função que colocamos na integral, temos:
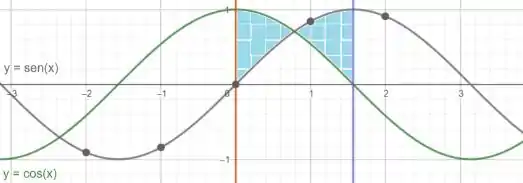
Entendeu direitinho? Responde aee ;)
