Desenhe o conjunto abaixo e calcule a área
- é o conjunto do plano limitado pelas retas , pelo eixo e pelo
gráfico de
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de cálculo . Temos que desenhar a nossa região
plano limitado pelas retas , pelo eixo e pelo gráfico de
e depois calcular a sua área.
O desenho da região fica da seguinte forma, as retas são as retas verticais
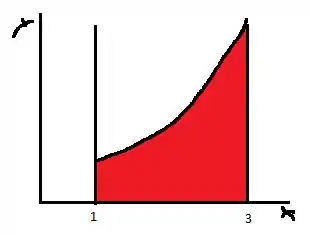
Onde a parte vermelha é a região . E a a sua área é dada pela área embaixo do gráfico , com
Passo 2
Calculando a área, temos
Usando a regra de integração do polinômio, obtemos:

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento acima