UFCG, Sem Campus, Cálculo Diferencial e Integral I, Listas Cálculo 1 - UAMat - Lista 5 - Integrais, Questão 6c
Desenhe o conjunto abaixo e calcule a área:
c) é o conjunto de todos tais que .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado pediu pra gente determinar a área e desenharmos a curva em que varia de até . Pra encontrar essa área vamos ter que calcular a integral de no intervalo em que varia.
Pra descobrir como tá variando, vamos fazer:
Dessa forma, temos ou . Então, com o auxílio de um software, plotamos a curva e conferimos se o resultado da área bate com a calculada.
Vamos lá!
Passo 2
Vamos calcular a integral:
Aplicando os intervalos de integração:
Plotando a função que nós colocamos na integral, temos:
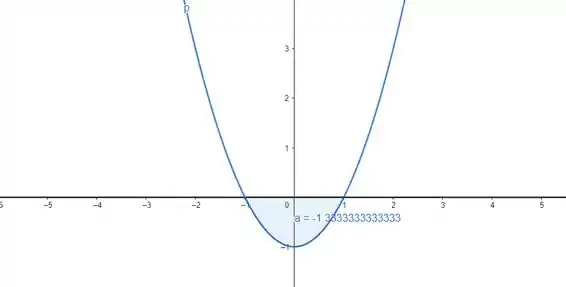
Repare que tem o mesmo valor calculado na integral, o valor é negativo apenas porque a gente tá considerando a função de cima, que é , menos a de baixo, que é . Mas de qualquer forma, nossa área é numericamente igual a , beleza?
Valeu, galera! Até a próxima! 😉