UFU, Sem Campus, Cálculo 2, P1 - 2022.1, Questão 4.
4 – Desenhe no plano cartesiano a região plana dada pelo conjunto dos pontos tais que , com , e calcule sua área.
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema, temos que desenhar a região limitada por e e também obter a área dessa região.
Tem ideia de como fazemos isso? 🤔
Para calcular a área da região abaixo de uma curva, podemos calcular a integral dessa curva.
Sabemos como é o gráfico de um , mas como deve ser o gráfico de um ?
Como estamos trabalhando em módulo e o cosseno tem partes onde é negativo, o que podemos fazer é espelhar essa parte negativa para a lado positivo de .
E também como está variando de a e o cosseno tem período de , então temos que ter dois períodos de de amplitude com os valores em módulo. Ou seja
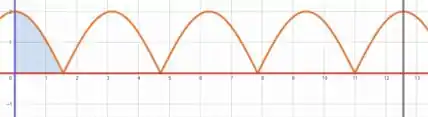
Consegue entender isso? 😉
Passo 2
Agora vamos calcular a área dessa região...
Não sabemos calcular a integral de , mas perceba que a região hachurada se repete vezes. Como nesse pequeno intervalo a curva acima é dada apenas por , então podemos calcular essa área e multiplicar por .
Sacou?
Se analisarmos, podemos ver que essa região corresponde a do período do , então está variando de a .
Pelo teorema fundamental do cálculo, a integral de é , então
Fim! Iae, o que achou? Responde Aí! 😁
