USP– Cálculo 1 – Lista 2 – Questão 3.2b
Desenhe a região e calcule sua área:
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou descomplicar para você! O problema deu essa região
E pediu para desenharmos a região e calcular a área!
Mas como resolver isso?
Precisamos fazer um esboço da região que pretendemos achar! Assim vamos verificar quais são os limites de integração e qual função está mais acima e mais abaixo, bem como dividir a região em várias caso precise! Vamos começar vendo uma função por uma:
então saca só como fica nossa região:
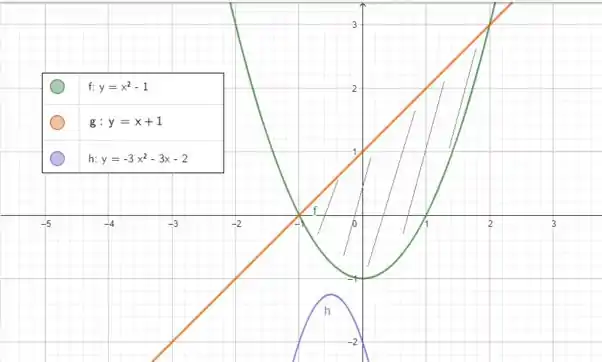
A região hachurada é nossa região A! Podemos verificar que a reta laranja está sempre por cima e a parábola por baixo, entre e
Beleza?
Nossa missão é montar a integral, acertar os limites de integração e partiu integrar!
É isso! Bora lá?
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Vamos começar montando nossa integral:
Beleza?
Agora vamos substituir as funções!
Organizando um pouco temos
Agora é só integrar!
Passo 3
Integrando temos
E por fim vamos aplicar nos limites!
E simplificando temos
Show! E é isso pessoal! Espero ter ajudado!