Determine a área hachurada a seguir:
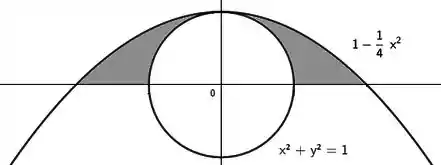
Passo 1
Essa questão já da a faca e o queijo pra gente. A faca seria a equação das curvas e o queijo, o desenho delas. Como a área hachurada está abaixo da curva , a área vai ser:
Peraí, quem é esse D aí? Veja bem, se quiséssemos a área abaixo da curva toda, íamos ter no desenho
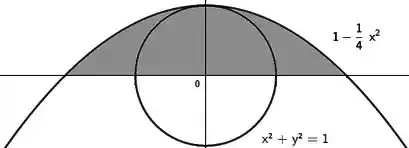
Mas como queremos:
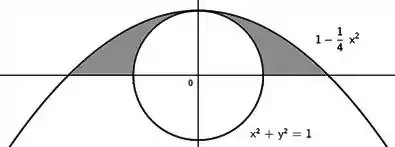
Vamos ter que subtrair a área :
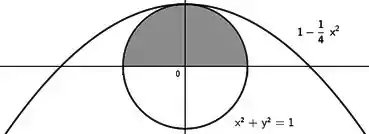
Então bora lá achar quem falta: A área e os limites de integração
Passo 2
Se olharmos com carinho pro desenho, vemos que a área está delimitada, em valores de , pelas raízes da curva. Pô, já que é assim, basta a gente achar as raízes e achamos os limites de integração. Partiu:
Sendo assim, os limites de integração vão ser:
Quanto a área , a gente poderia integrar, mas ficaria um pouco mais complicado. A sagacidade é ver que:
Representa uma circunferência de raio centrada na origem! Como a área é metade da área da circunferência, temos:
Então já temos tudo pra calcular a área, que vai ser:
Passo 3
Agora é só por a mão na massa. Fazendo a integral, vamos ter: