3) Determine a área da região delimitada por:
Passo 1
Bora lá então. A primeira coisa que temos que notar é que existem duas funções de que delimitam esse área, então tamos num exercício de área entre curvas.
Em exercícios assim é bom a gente se ligar em duas coisas:
- Qual curva tá por cima e qual tá por baixo
- Quando cada curva está abaixo do eixo
Então bora lá. Pra começar, como são funções trigonométricas, vamos olhar o círculo trigonométrico:
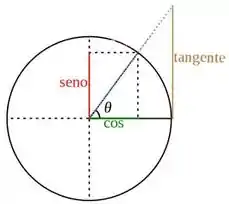
Vamos olhar o círculo só para valores de arco entre e , beleza? Afinal, as retas:
Também delimitam a região. Show de bola. Perceba que o aumenta conforme o arco aumenta e o diminui conforme o arco aumenta até chegar em . Oras, então vai ter algum momento em que as curvas vão se cruzar. Bora achar quando:
Se em as curvas se cruzam, então nesse ponto passa a ficar por cima de ! Um esboço do gráfico das curvas seria:
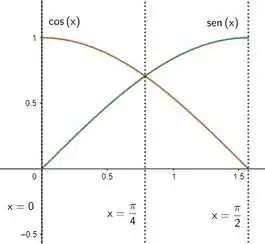
E como a questão pede a área delimitada pelas duas curvas e as retas e , então a área a ser calculada vai ser:
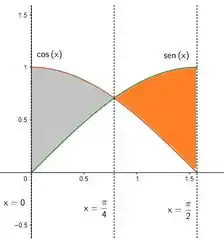
Vamos calcular a área de cada uma das cores e depois somar agora.
Passo 2
Começando pela área cinza, veja bem. A gente pode entender ela como a subtração da área azul menos a área amarela:
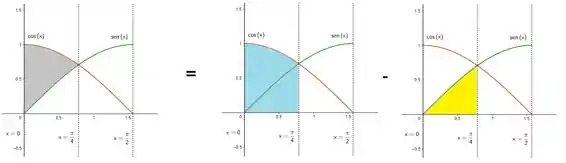
A área azul nada mais é do que a integral de e a área amarela que a integral de viu? Isso pros mesmos dois limites de integração. Vamos ter então pra azul:
E pra área amarela:
E logo:
Passo 3
Agora pra gente ver a área da região laranja, podemos usar a mesma ideia em! Vamos ter que a área laranja é a área roxa menos a área rosa:
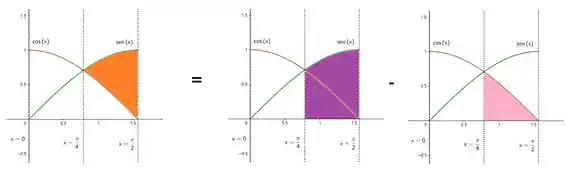
Como a área roxa está abaixo da curva de , vamos ter:
E pra área rosa agora:
Considerando a área laranja como um todo, temos:
Passo 4
E pra fechar com chave de ouro é spo juntar a área das curvas laranja e cinza que juntos são exatamente a área delimitada por todas as curvas. Vamos ter:
Se a gente olhar bem pro esboço da até pra ver que a região é simétrica em relação à . E daí? Bem, isso pouparia algumas contas mas não mostraria o cálculo em ação haha