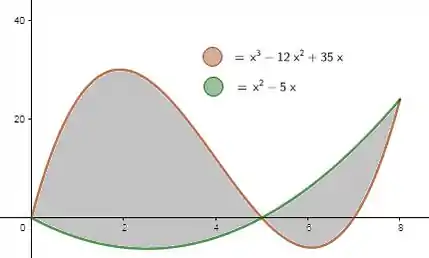
Determine a área da região limitada pelas curvas e
Passo 1
A primeira coisa que a gente tem que notar é que se a questão ta pedindo área delimitada pelas curvas, é porque elas se cruzam. O truque vai ser saber em qual ponto! Pra isso, vamos precisar igualar esses dosi caras aí. Vamos ter:
Colocando em evidência:
Opa, então é um ponto em que as curvas se cruzam. Ok, mas não é o único, porque podemos ter também:
Como nesse caso temos um polinômio de segundo grau, vale usar Bháskara! Seja:
As raízes do polinômio vão ser:
Então o polinômio pode ser escrito como:
O que quer dizer nada mais nada menos que:
São outros dois pontos onde as curvas se encontram.
Passo 2
Uma coisa que precisamos também saber são as raízes das próprias curvas! Afinal, como vamos usar integrais pra calcular a área, temos que saber quando a curva está abaixo do eixo pra não calcular áreas negativas sem querer! Pra primeira curva:
Colocando em evidência de novo:
E sendo:
As raízes vão ser:
Reescrevemos como:
As raízes vão ser então:
Pra segunda curva, vamos ter:
E se colocarmos o em evidência, vemos já as raízes:
Passo 3
Show, vamos ver todos os pontos interessantes que achamos:
Esses pontos são raízes e pontos em que as curvas se encontram. Bora analisar o que acontece com as curvas nos intervalos que envolvem esses pontos. São eles:
Vamos ver o primeiro intervalo então. Olha o que acontece se, nas curvas, escolhermos , um ponto desse intervalo:
Opa, então não só a curva está por cima da curva como está abaixo do eixo . Pra esse intervalo então, a área vai ser:
Lembrando que o sinal de negativo tá aí pra gente não calcular áreas negativas! Olhando agora pro segundo intervalo, escolhendo , por exemplo, temos:
Opa, agora invertemos! está por cima de e abaixo do eixo . A área vai ser então:
E pré fecharmos, vamos ver o último intervalo. Escolhendo por exemplo, temos:
Dessa vez temos as duas curvas acima do eixo ! Então a área vai ser a área da curva que está por cima, nesse caso , menos a área da curva que está por baixo, nesse caso :
Passo 4
Agora é só calcular a área e partir pro abraço. A área total vai ser:
Substituindo, temos:
Das propriedades das integrais, simplificamos:
Sendo a integral indefinida:
Temos:
Calculando as integrais indefinidas
Vamos ter que:
E logo:
Calculamos:
A área total vai ficar:
Resposta