UFPB, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - Profº Pedro Hinojosa - Lista de Exercícios 3, Questão 1a
Determine a área da região limitada pelas curvas dadas em cada caso:
a) , , e
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente encontrar o valor da área na região limitada pela parábola ) , a reta e as retas verticais e . Nossa região fica assim:
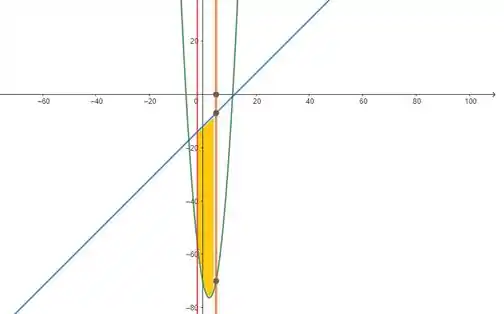
Por definição, a área limitadas pelas curvas e e pelas retas e , onde e são funções contínuas e para todo no intervalo , é dada por:
Aqui é a função que limita superiormente nossa região, no nosso caso, quem tá por cima é a função . E como limita a região inferiormente, temos . Nosso intervalo de integração é definido pelas retas e . Então, para determinar a área, nós só vamos precisar calcular a integral:
Vamos lá!
Passo 2
Vamos arrumar nossa integral:
Somando os termos semelhantes:
Como a integral da soma é igual a soma das integrais, podemos escrever:
Agora podemos calcular cada integral usando a regrinha da potência ():
Aplicando os limites de integração, temos:
E temos nossa área:
Prontinho, galera! Até a próxima! 😉