UFPB, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - Profº Pedro Hinojosa - Lista de Exercícios 3, Questão 1b
Determine a área da região limitada pelas curvas dadas em cada caso:
b) , e
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente encontrar o valor da área na região limitada pela curva e pelas retas e . Nossa região fica assim:
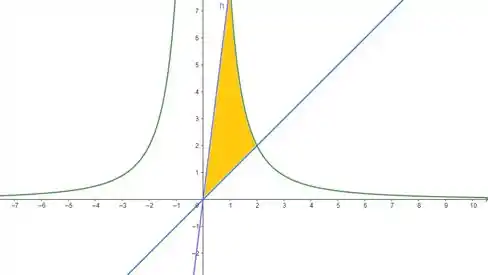
Como temos três curvas, vamos dividir nossa área em duas partes. Primeiro, vamos encontrar a interseção entre a e e calcular a integral dupla na região que vamos chamar de . Em seguida, vamos encontrar a interseção entre e , pra calcular a integral dupla na região que vamos chamar de . Então, nossa área é calculada na forma:
Vamos lá!
Passo 2
Vamos começar encontrando a interseção entre e :
Então, temos o ponto de interseção e a região dada por:
Agora na interseção entre as curvas e , temos:
E temos o ponto de interseção e a região dada por:
Passo 3
Vamos montar nossa integral então:
Calculando a integral em relação a , temos:
Agora vamos aplicar os limites de integração:
Agora vamos integrar em relação a :
Aplicando os limites de integração, temos:
Prontinho, galera! Até a próxima! 😉