UFPB, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - Profº Pedro Hinojosa - Lista de Exercícios 3, Questão 1d
Determine a área da região limitada pelas curvas dadas em cada caso:
d) , e
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente encontrar o valor da área na região limitada entre as parábolas e e o eixo . Nossa região, então, é essa em amarelo:
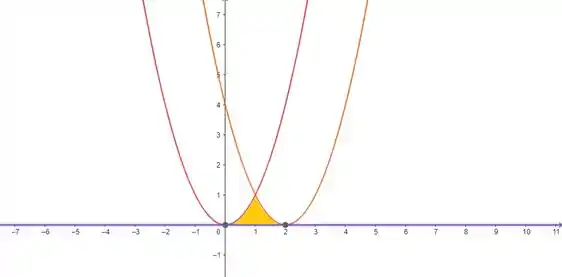
Repare que de até , nós temos limitando nossa região superiormente. De até , nós temos limitando a região superiormente, e limitando a região inferiormente nos dois casos. Então, nossa área pode ser dividida nessas duas partes, de modo que a gente consiga resolver a integral:
Então, vamos lá calcular a área através da integral.
Passo 2
Arrumando um pouquinho as integrais, vamos ter:
Integrando em relação a , temos:
Aplicando os limites de integração:
Prontinho, galera! Até a próxima! 😉
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x