UFPB, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - Profº Pedro Hinojosa - Lista de Exercícios 3, Questão 1c
1 - Determine a área da região limitada pelas curvas dadas em cada caso
c) e
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema queremos obter a área determinada pela região limitada pelas curvas e .
E aí, tem ideia de como fazemos isso? 🤔
Para obter a área entre duas curvas, podemos usar o método de integral dupla, ou seja
E nosso trabalho é conseguir descrever a região para definir os limites de integração.
Sacou? Bora começar!
Passo 2
Vamos começar definindo visualmente a região . Plotando as curvas das equações dadas temos
Essa parte não ficou muito clara na questão, mas considerando que a região é definida para , temos
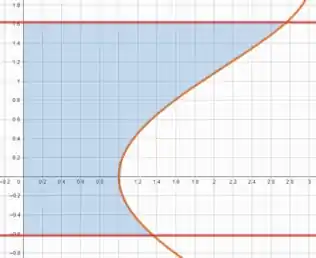
Assim, podemos definir os limites de integração de como e . Já em , podemos definir os limites de integração como e
Tranquilo até aqui? 😎
Passo 3
Dessa maneira, montando nossa integral de área , temos
Integrando com relação a , temos
Aplicando os limites de integração
Agora integrando o resultado com relação a
Aplicando os limites de integração...
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
