Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 266123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

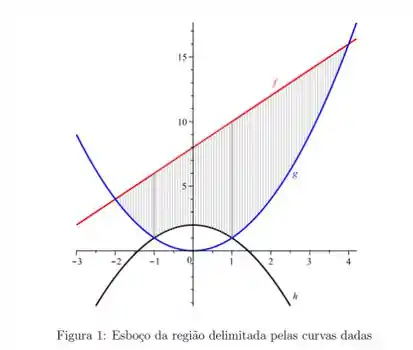
Determine a área da região limitada exatamente pelas três curvas

y = x ² ,   y = 2 - x ²   e   y = 2 x + 8

Passo 1

Queremos a área da região limitada pelas curvas e já sabemos que isso pode ser calculado através de integrais definidas. Observe no esboço dado no enunciado que a curva de função f ( x ) = 2 x + 8 é maior que a curva g x = x ² no intervalo - 2 ,   4 , logo, nesse intervalo, a área desejada pode ser calculada por uma integral que faça a subtração

f x - g ( x )

Além disso, é necessário excluir a área entre as curvas h e g . Já que no intervalo - 1 ,   1 a curva h é maior que a curva g , teremos que fazer uma integral com a seguinte subtração

h x - g ( x )

Passo 2

Agora vamos montar as integrais e calcular a área

A = ∫ - 2 4 f x - g x d x - ∫ - 1 1 h x - g x d x

A = ∫ - 2 4 ( 2 x + 8 - x 2 ) d x - ∫ - 1 1 ( 2 - x 2 - x 2 ) d x

A = 2 x 2 2 + 8 x - x 3 3 - 2 4 - 2 x - 2 x 3 3 - 1 1

A = 60 - 64 3 - 16 3

A = 100 3 u . a

Resposta

A = 100 3 u . a

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x