USP– Cálculo 1 – Lista 2 – Questão 3.4
Determine a área da região plana delimitada pela curva e por sua reta tangente no ponto de abscissa
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou descomplicar para você! O problema quer que a gente ache a área delimitada pela curva
E pela reta tangente a essa curva no ponto
Então antes de mais nada precisamos achar essa reta tangente! E depois? Depois é só esboçar a região, montar a integral e partiu resolver!
É isso! Bora lá?
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Vamos começar achando a reta tangente
E no ponto
Beleza?
Agora nossa reta tangente é
Temos que e , aí é
Agora é só jogar na equação da reta
Passo 3
A região que queremos envolve a curva
E a reta
Fazendo um esboço dessas curvas temos o seguinte
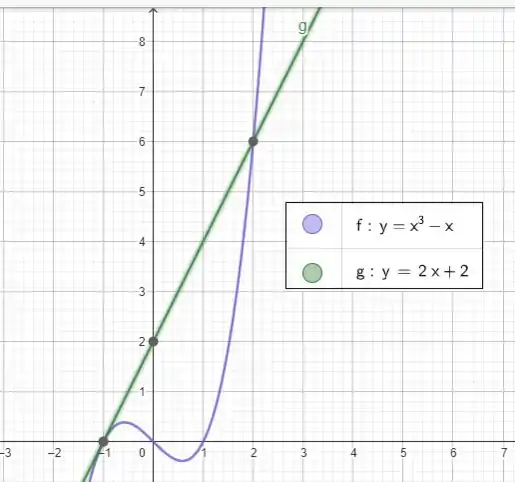
Sendo assim a integral que calcula essa área é
Passo 4
Agora e só resolver e aplicar nos limites de integração!
Aplicando os limites
Beleza?
Show! E é isso pessoal! Espero ter ajudado!