UFBA, Sem Campus, Cálculo B, Listas de Cálculo B - UFBA - Lista 1, Questão 3.3h
Determine o centróide da região limitada por:
Passo 1
Eaew, tudo certinho?
Nós temos que determinar o centróide da região delimitada pelas curvas
, , e
esta é uma região arbitrária, que pode ser visualizada como
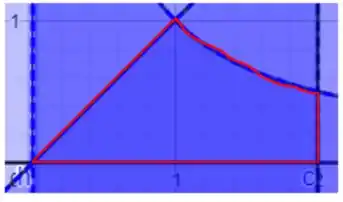
o centróide aqui será indicado com um ponto com duas coordenadas (estamos em uma região bidimensional), estas coordenadas são calculadas usando
e
Ou seja, nós temos duas integrais para resolver, isso será feito mudando o infinitesimal de área que escolhemos! Saca só!
Passo 2
Para integrarmos primeiro em , vamos escolher um infinitesimal de área com largura como indicado
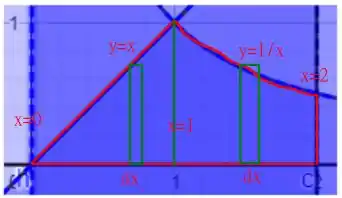
Temos que calcular individualmente as integrais para a região à esquerda de e a direita de pois o infinitesimal de área muda para cada um deles! Temos que
e
de forma que a integral de área é dada por
usando as integrais conhecidas, temos que
ou simplesmente
Eu calculei essa área primeiro pois será utilizada em ambas as coordenadas, você pode calcular ela integrando com um infinitesimal em da mesma forma! Agora, vamos calcular as coordenadas!
Passo 3
Para calcular a coordenada temos que calcular a seguinte relação
o é apenas para diferenciar todos os que aparecem dentro da integral. Podemos igualmente escrever a expressão como
obtendo então a integral
que podem ser resolvidas diretamente, obtendo
de forma que temos
Vamos calcular a coordenada agora!
Passo 4
Para integrar em precisamos visualizar outro infinitesimal, note que
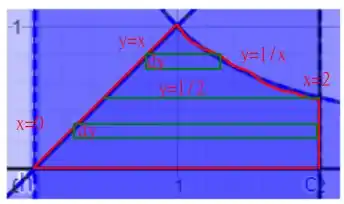
Note que a linha horizontal verde separa a região em duas! Eu fiz isso pois a definição de altura muda em cada região! Temos as seguintes integrais
distribuindo, temos que
Estas integrais são conhecidas, temos que
expandindo os limites de integração, temos que
simplificando, nós obtemos
Nosso centróide está então em
A questão foi isso! Te vejo na próxima! Tchau Tchau!