Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 227123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Área entre Curvas

Determine o valor de a e b e calcule a área da região destacada na figura abaixo:

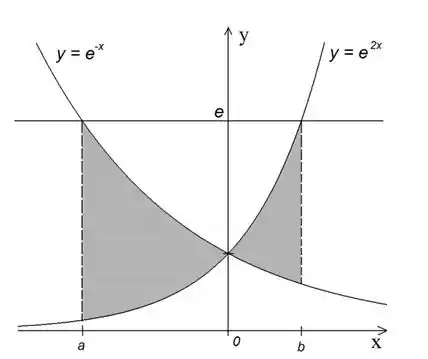
Passo 1

O ponto x = a é onde a reta y = e encontra com a função y = e - x . Portanto, igualamos:

e - a = e

Puxando o logaritmo, obtemos:

- a = 1 → a = - 1

Passo 2

De maneira análoga, o ponto x = b é quando a reta y = e encontra com a função y = e 2 x . Igualamos então:

e 2 b = e

Puxando o logaritmo obtemos:

2 b = 1 → b = 1 2

Passo 3

Para calcular a área, fazemos a soma das integrais:

A = ∫ - 1 0 e - x - e 2 x d x + ∫ 0 1 2 e 2 x - e - x d x

Fazendo a indefinida, temos:

I * = ∫ e - x - e 2 x d x = - e - x - e 2 x 2 + C

Plugando os valores temos que:

A = - e - x + e 2 x 2 - 1 0 + e - x + e 2 x 2 0 1 2

A = - 1 + 1 2 - e - 1 2 e 2 + e - 1 2 + e 2 - 1 - 1 2

Arrumando:

A = - 1 - 1 2 + e + 1 2 e 2 + e - 1 2 + e 2 - 1 - 1 2

A = - 3 + 3 2 e + 1 2 e 2 + e - 1 2

Resposta

- 3 + 1 2 e 2 + 1 e + 3 2 e

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x