Determine o valor de para o qual o ponto de insterseção dos gráficos das funções definidas no intervalo , divida a região entre eles em duas regiões de mesma área. Vide figura abaixo.
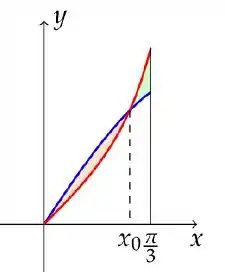
Passo 1
Bom, medimos uma área abaixo do gráfico calulando sua integral, certo? Mas a área que estamos procurando está entre duas curvas. Então fazemos a de cima MENOS a debaixo. Com isso a gente já quase concluiu a questão. O único outro porém aí é que ele quer que aquelas duas áreas ali acima sejam iguais, logo, escrevemos assim
Agora é só calcularmos isso pra encontrar o valor de
Passo 2
Como é uma constante, podemos tirá-la da integral. Com isso temos já tabelado as integrais de sem e da tangente.
Passo 3
Agora é só isolar o . Simples assim.
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x