UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Matheus Nunes - Lista 7, Questão 8i
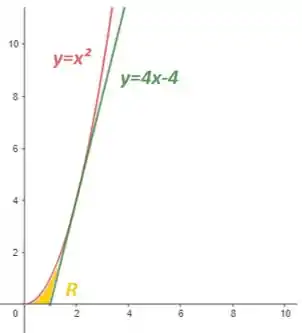
EE3. 2012.2 Esboce a região do plano delimitada pela parábola , pela reta e pelo eixo .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para esboçar as regiões entre os gráficos , e o eixo das abscissas.
Para isso, temos que entender graficamente cada equação e depois vamos juntar tudo, belezinha?
E aí?? Bora lá??
Passo 2
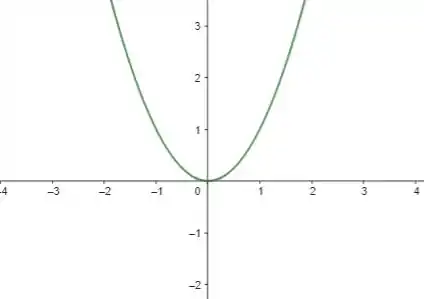
Primeiramente vamos analisar .
De cara, vemos que trata-se de uma equação do segundo grau, ou seja, uma parábola com vértice em e com concavidade voltada para cima.
Graficamente, temos:
Passo 3
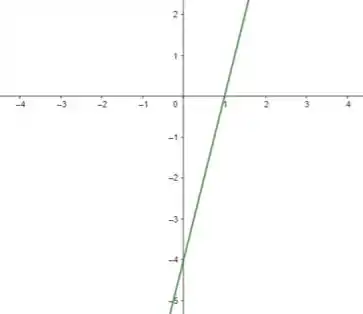
Para segunda equação, temos .
Vemos que trata-se de uma equação do primeiro grau, ou seja, uma reta.
E essa reta tem inclinação positiva, interceptando o eixo no ponto e que se estende para cima, ou seja:
Passo 4
Dessa forma, juntando os gráficos e considerando apenas o eixo positivo das abscissas, temos o plano :
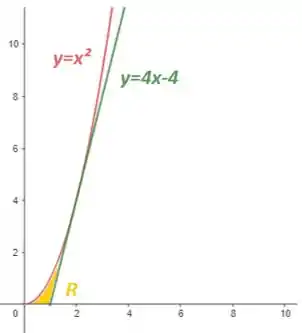
Entendeu direitinho? Responde aee ;)
Resposta
