UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Matheus Nunes - Lista 7, Questão 8h
EE3. 2015.2 Considere a região no primeiro quadrante limitada pelas curvas , e . Esboce a região e calcule sua área.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para esboçar as regiões entre os gráficos , e .
Além disso, a questão também nos pede a área delimitada pelas curvas.
Plotando primeiramente os dois gráficos e colocando em evidência as regiões delimitadas, temos:
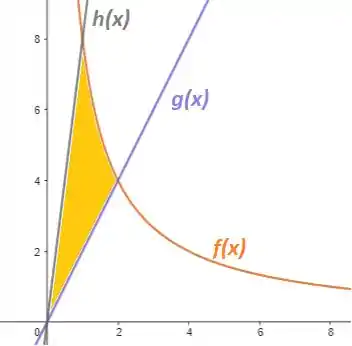
Para descobrir a área de cada região, primeiro temos que encontrar os pontos de interseção para descobrirmos os limites de integração.
Depois, basta aplicarmos nas integrais!!
E aí?? Bora lá??
Passo 2
Primeiramente vamos descobrir os pontos de interseção entre e :
Logo, .
Assim, temos o ponto .
Já para e , temos:
Logo, .
Assim, temos o ponto .
Por fim, igualando e , temos:
Passo 3
Dessa forma, podemos descobrir nossa área fazendo as seguintes integrais:
Entendeu direitinho? Responde aee ;)
