UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Matheus Nunes - Lista 7, Questão 8a
EE3. 2019.2 Esboce as regiões do plano delimitadas pelos gráficos de e e calcule a área de cada uma dessas regiões.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para esboçar as regiões entre os gráficos e . Além disso, a questão também nos pede a área.
Plotando primeiramente os dois gráficos e colocando em evidência as regiões delimitadas, temos:
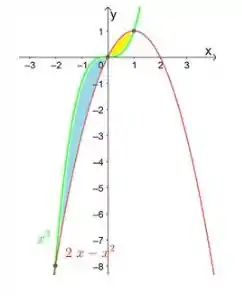
Para descobrir a área de cada região, fazemos da seguinte forma:
Onde representa a função que limita região por cima e , a nossa função por baixo.
Obs: Repara que isso muda da região azul para a região amarela!
E aí?? Bora lá??
Passo 2
Dessa forma, fazendo para a região azul, temos:
Passo 3
Já para a região amarela, temos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x