UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Matheus Nunes - Lista 7, Questão 8d
EE3. 2019.1 Esboce as regiões do plano delimitadas pelos gráficos de e pelo semicírculo superior de raio centrado na origem.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para esboçar a região entre os gráficos e (que é a equação do semicírculo de raio ).
Plotando primeiramente os dois gráficos, temos:
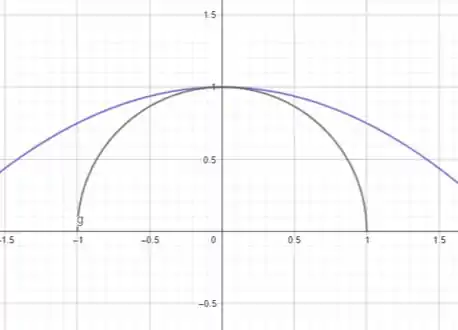
Passo 2
Ao observarmos o gráfico gerado, vemos que não há área delimitada, pois os gráficos das funções encontram-se em apenas um ponto (em ).
Entendeu direitinho? Responde aee ;)
Resposta
Não há área interceptada
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x