Encontrar a área da região delimitada pelo laço interno da limaçon . Grafique.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular a área da região polar dada pela equação . Em coordenadas polares a área da região é dada pela integral:
Onde é a função que determina como o raio da curva varia em relação ao ângulo no intervalo .
Então, vamos lá montar nossa integral!
Passo 2
Nós temos uma equação do tipo , com e , logo e temos um limaçon com um laço, simétrico em relação ao eixo :
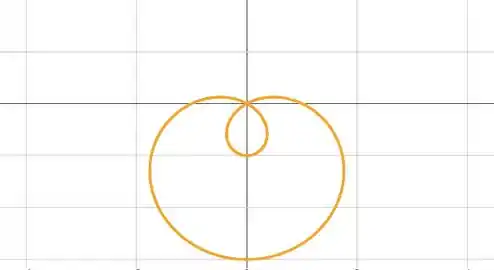
Como queremos apenas a área do laço interno do limaçon, vamos usar o fato dele ser simétrico em relação ao eixo , calculando a área multiplicando por dois no intervalo . Assim, teremos:
Separando os termos, temos as integrais:
Calculando as integrais, temos:
Aplicando os intervalos de integração:
Prontinho, galera! Até a próxima! 😉