UFPB, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - Lista de Exercícios 2, Questão 4
Encontre a área limitada pelas curvas e .
Passo 1
Eaee!!! Belezinha? Bom...a questão nos dá duas funções e nos pede calcular a área da região limitada pelas funções.
Primeiramente, plotando o gráfico com as duas funções, temos:
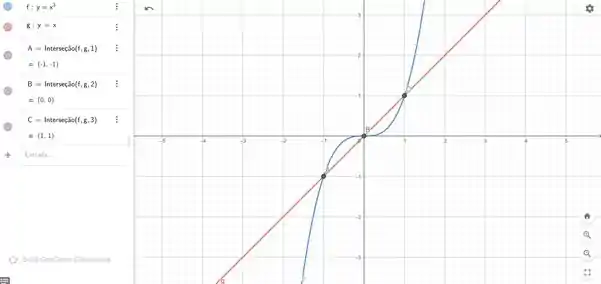
Como as áreas são iguais entre os trechos e , então podemos calcular a integral de apenas um dos trechos e multiplicar por para encontrarmos a área :
Não entendeu? Então bora junto 😉
Passo 2
Bom... dessa forma, resolvendo a integral, temos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x