Encontre a área da região limitada acima por , abaixo por e nas laterais por e .
Passo 1
O primeiro passo nesse caso é fazer um esboço de cada uma dessas equações no plano.
Começando pelo mais fácil: e são só duas retas verticais cruzando esses pontos.
Para fazer o esboço da de forma útil, é uma boa ideia calcular e , e traçar uma reta entre esses dois pontos.
E para a também, você sabe que é uma parábola por conta do , então calcule que e e faça uma parábola razoável que passe por esses dois pontos.
Você deve ficar com algum parecido com isso aqui:
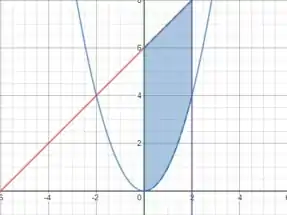
E o nosso objetivo é calcular essa área que está em azul.
Passo 2
Percebe que essa região azul é simplesmente a área embaixo da reta vermelha menos a área em baixo da parábola azul? Tudo isso no intervalo .
Mas “área embaixo da função” é exatamente o que a integral calcula, então escrevendo isso como integrais, vamos achar o seguinte:
Ótimo, agora é só substituir:
E agora ficamos com a integral de um polinômio. Lembra como integra uma função desse tipo? A lógica é essa aqui:
Passo 3
Ótimo, agora vamos aplicar essas técnicas para calcular a área:
Como todas as integrais vão ser nulas quando , fica fácil substituir os limites:
Pronto, essa é a área da nossa região.
Resposta
A área da região é