UFPA, Sem Campus, Cálculo I, Listas de Cálculo 1 - Profº Arthur Fontana - Lista 3, Questão 4
Encontre a área da região limitada pelo gráfico de , o eixo dos e as retas verticais e .
(Obs: Antes de resolver a integral, faça um esboço do gráfico, para verificar a região a ser calculada).
Passo 1
Eaee!!! Belezinha? Bom... a questão quer que esbocemos e calculemos a área correspondente da seguinte função:
Mas detalhe... queremos encontrar a área definida entre essa função e o eixo dos e as retas verticais e .
Eaí? Bora lá resolver?
😉
Passo 2
Então... vamos primeiro esboçar a função quadrática :
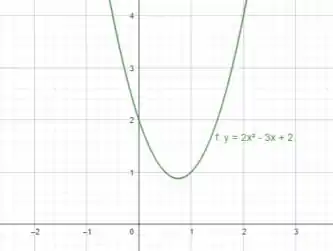
Adicionando as informações de que queremos encontrar a área definida entre essa função e o eixo dos e as retas verticais e , temos:
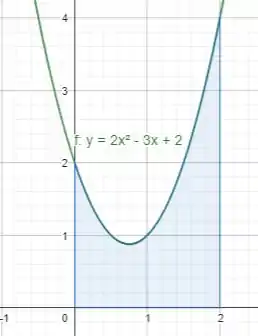
Agora vamos calcular!!
Passo 3
Resolvendo a integral, temos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x