Encontre a área da região limitada pelo gráfico das funções e para .
Passo 1
Fala galera, tudo bem? Vamos resolver essa questão juntos?
 Segura minha mão e vem comigo!
Segura minha mão e vem comigo!
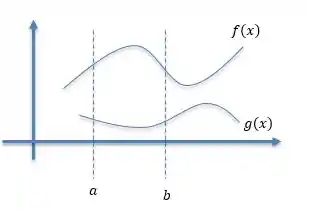
E essa área é dada por:
É a integral da função de cima menos a função de baixo. Então o problema está na gente descobrir quem é que está em cima e quem é que está embaixo.
Será que a gente pode simplesmente calcular o valor das duas funções em um ponto, pra ver quem é maior? Ou então será que podemos calcular as duas áreas e ver quem é maior? Não, nem sempre vai ser tão simples assim. Não é sempre que uma função é maior que a outra em todo o intervalo. Pode acontecer delas se cruzarem e, em uma hora, a f(x) estar em cima da g(x) e em outra hora, ser ao contrário. Esquisito? Vamos ver se isso acontece no próximo passo.
Passo 2
Vamos ver se há algum ponto onde essas duas curvas se encontram, pra descobrir se uma delas fica em cima todo o tempo, ou se elas cruzam e invertem. Pra ver se duas funções se cruzam, a gente iguala né:
Então a gente sabe que quando o cosseno vale essas funções de cruzam, ou seja, em . Isso quer dizer que em há uma quebra no intervalo. Para saber quem é maior antes e depois de , é só pegar um ponto e testar as duas.
Antes de vou escolher :
Logo, de até quem está por cima é .
Para o trecho depois de , vamos olhar pro extremo do intervalo . Quando vai se aproximando de , a função vai tendendo ao zero, pois , já a função vai tendendo a 1. Então, em a função é maior do que a função , ou seja, ela fica em cima, no gráfico.
Passo 3
Fazendo um gráfico dessa área a gente tem o seguinte:
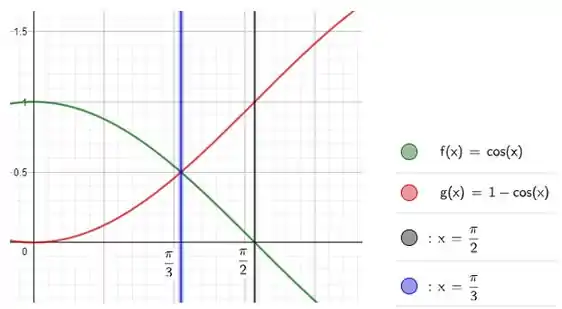
Entre e a curva vertical azul a curva verde (que é a ) está acima da curva vermelha (que é a ). Bem em essas duas curvas tem o mesmo valor . E entre e a função vermelha está por cima da função verde.
Assim vai ser preciso quebrar essa região em duas: uma de até e outra de até . Saca só:
Reparem que o integrando acompanha a troca de limites. A função que está por cima MENOS a função que está por baixo, beleza?

Passo 4
Agora vamos substituir as funções e nos integrandos:
Aí nossa área fica assim:
Agrupando os termos semelhantes temos o seguinte:
E agora é só resolver essas integrais!!
 Calma, vamos juntos!
Calma, vamos juntos!
Passo 5
Começando pela primeira da direita:
A integral do cosseno é o seno, e a integral de é , daí ficamos com o seguinte:
Passo 6
E agora a outra integral:
Passo 7
Estamos quase lá! Agora precisamos juntar os resultados dos passos 5 e 6:
E simplificar o máximo que der! Juntando as raízes e fazendo o mmc nos termos que tem :
Tranquilo?
Espero ter ajudado!
