UFBA, Sem Campus, Cálculo B, Listas de Cálculo B - UFBA - Lista 1, Questão 1.4
Encontre a área da região limitada pela parábola , pela reta tangente a esta parábola em e pelo eixo .
Passo 1
Fala aí pessoal, tudo bom com vocês?
Nessa questão temos uma região limitada por:
- uma parábola:
- a reta tangente a essa parábola em ;
- eixo .
Queremos calcular a área dessa região.
Para fazer isso, vamos começar esboçando melhor essa região e depois podemos usar o recurso da integral. Se uma região é definida de tal forma que:
Podemos escrever que a área dessa região é dada por:
onde e são determinados pela intersecção de e .
Massa!
Vamo nessa!
Passo 2
Bom, a parábola é tangente ao eixo em e simétrica ao eixo .
Já a tangente à parábola em pode ser dada pela derivada da equação da parábola.
Esse é o coeficiente angular da reta. Como queremos no ponto , temos:
Daí, a reta:
Será dada por:
Como pertence à reta:
Portanto, a equação da reta tangente à parábola é dada por:
Agora vamos esboçar essas duas curvas, junto com o eixo , em um mesmo gráfico.
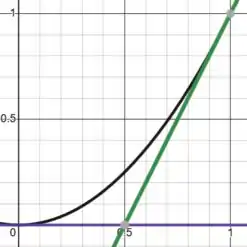
Muito bom!
Passo 3
Para calcular a área dessa região, vamos usar aquela ideia que comentamos no passo .
Nesse caso, a função que delimita a nossa região inferiormente com relação ao eixo é a parábola. Logo:
Então:
Já a função que delimita essa região superiormente é a reta tangente, assim:
Então:
Como a nossa região vai de até , substituindo na integral, temos:
Logo:
Aeee! Terminamos!
Espero que vocês tenham entendido bem direitinho, até a próxima 😉