Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 381123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UTFPR, Sem Campus, Cálculo Diferencial e Integral 1, Provas - Profª Lilian Brambila - P3 2023.1

Encontre o volume do sólido pela rotação ao redor do eixo x da região determinada pelas curvas y   =   s e n ( x ) ,   y   =   c o s   ( x ) , com 0   ≤   x   ≤   π / 4 . Faça um esboço da região.

Passo 1

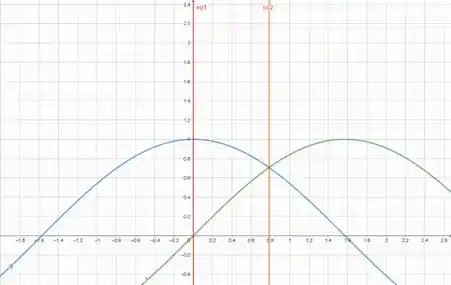
A região que iremos rotacionar em torno do eixo x é a região compreendida pela reta vermelha e laranja na vertical e pelas equações de reta azul e verde.

O volume de um solido de rotação em relação ao eixo x é dado por,

V = π ∫ a b f x 2 - g x 2 d x

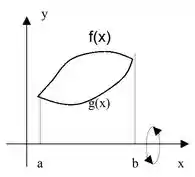
Passo 2

Calculando, temos

V = π ∫ 0 π 4 cos 2 ⁡ x - sin 2 ⁡ x d x

Sabemos que a identidade trigonométrica cos ⁡ 2 x = cos 2 ⁡ x - sin 2 ⁡ x

V = π ∫ 0 π 4 cos ⁡ 2 x d x

V = π 2 sin ⁡ 2 x ​ 0 π 4  

V = π 2   u . v

E aqui terminamos nossa resolução, um forte abraço meu caro colega e até uma próxima.

Resposta

V = π 2   u . v

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x