UFPA, Sem Campus, Cálculo I, Listas de Cálculo 1 - Profº Arthur Fontana - Lista 3, Questão 3d
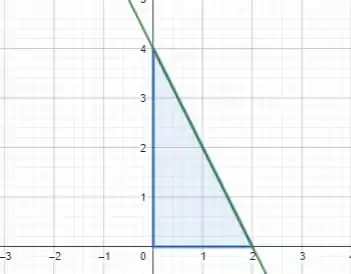
Esboce a região correspondente a cada uma das integrais definidas, depois calcule as integrais.
d)
Passo 1
Eaee!!! Belezinha? Bom... a questão quer que esbocemos a área correspondente da seguinte integral definida:
Para isso, temos que plotar a função contida dentro da integral e aplicar os limites de integração!!
Lembrando que a integral definida tem a seguinte forma:
Em seguida, a questão também nos pede para resolver a integral.
Eaí? Bora lá resolver?
😉
Passo 2
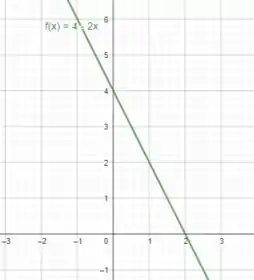
Então... podemos perceber que a função contida na integral é:
Assim, plotando, temos:
Aplicando os intervalos de integração, temos a seguinte região:
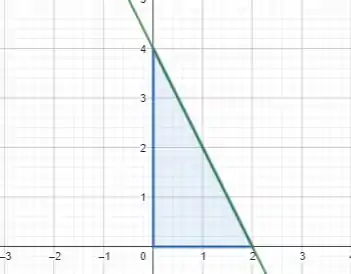
Agora vamos calcular!!
Passo 3
Resolvendo a integral, temos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x