UFU, Sem Campus, Cálculo 2, Listas de C2 - Profª Ana Paula - Lista 7 - Integrais Duplas, Questão 10b
Esboce a região cuja área é dada pela integral e calcule-a.
b)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular a integral dupla e esboçar a região que ela representa. Calcular a integral é tranquilo, a parte mais chatinha é o esboço do gráfico.
Mas calma, porque basta a gente perceber como as variáveis e est��o variando, de acordo com a ordem de integração. Repare que para o raio , temos os seguintes limites:
E o ângulo tá variando dentro do intervalo:
Então, vamos usar isso para esboçar nosso gráfico no plano cartesiano e, em seguida, calcular nossa integral.
Vamos lá!
Passo 2
Já vimos que o raio está variando de até . Nessa segunda expressão, temos uma circunferência com centro na reta e raio , ou seja:
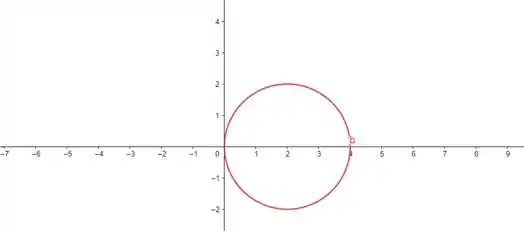
Mas a gente não quer toda a circunferência, a gente quer só a parte em que o ângulo varia de até . Então, nossa região vai ser essa em amarelo:
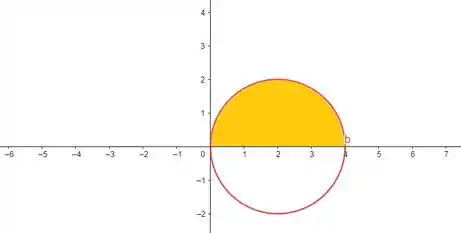
Passo 3
Agora que já esboçamos gráfico da nossa região, vamos calcular a nossa integral:
Integrando primeiro em relação a :
Aplicando os intervalos de integração em :
Agora integrando em relação a :
E aplicando os limites de integração em :
Valeu, galera! Até a próxima! 😉