Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região
(8) , ,
Passo 1
Faaala, galeeera! Tudo tranquilo por aí?
O objetivo principal dessa questão é calcular a área de uma região por meio da integração. Para isso precisamos esboçar as funções para entender a delimitação do local. Por fim, vamos desenhar o retângulo com sua altura e largura.
Primeiramente, devemos esboçar as funções. Veja a figura abaixo que representa a interseção entre elas.
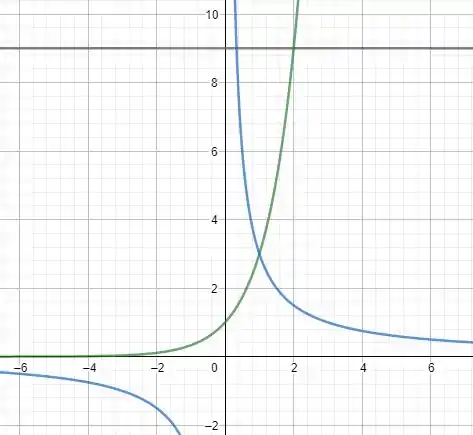
Para essa questão vamos dividir a área em duas, como mostra a figura abaixo
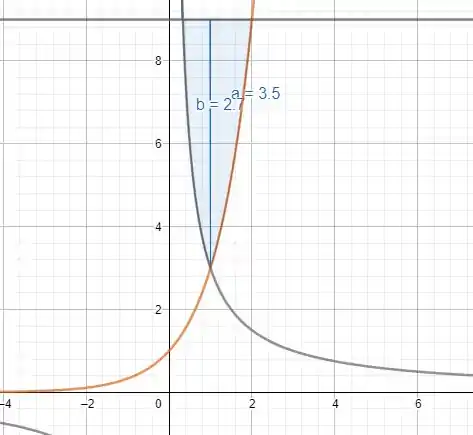
Passo 2
Podemos agora calcular a interseção entre as funções, ou seja, o ponto em que as funções se cruzam. Observe que as funções se cruzam em determinados pontos. Vamos calcular as interseções?
Calculando a interseção entre e , temos
Aplicando a função logarítmica em ambos os lados
Subtraindo em ambos os lados:
Aplicando a função exponencial em ambos os lados:
Logo, o único valor que satisfaz a igualdade é
Área 1:
Para a primeira área, devemos calcular a interseção entre e .
Encontrando :
Primeiramente, devemos igualar as funções
Logo, o intervalo de integração dessa área será de até .
Área 2:
Para a segunda área, devemos calcular a interseção entre e .
Encontrando :
Devemos igualar as funções
Logo, o intervalo de integração dessa área será de até .
Passo 3
O próximo passo é calcular a área da região por meio da integração. Sabemos que a área é dada por:
Em que, a f(x) é a função que delimita a parte superior da área e g(x) é a função que limita a parte inferior da área. Como mostra a figura abaixo
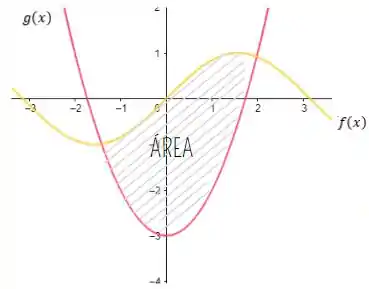
Substituindo os dados para calcular a primeira área, temos:
Calculando a integral
Substituindo os dados para calcular a segunda área, temos:
Calculando a integral
Note que: Dividimos em duas áreas. Logo, devemos somar o valor obtido em cada uma para encontrar o valor da área total, beleza?
Até a próxima!
