Esboce a região e encontre a sua área:
Passo 1
Olá galerinha, como vocês estão?
Nessa questão recebemos uma região do plano real, determinada pela desigualdade:
A partir disso, precisamos esboçar e determinar a área de .
Para fazer isso, podemos usar o recurso da integral. Se uma região é definida de tal forma que:
Podemos escrever que a área dessa região é dada por:
onde e são determinados pela intersecção de e .
Massa!
Vamo nessa!
Passo 2
Vamos começar esboçando a nossa região, temos a desigualdade:
Olhando para a desigualdade da esquerda:
Ou seja, é a região acima da parábola determinada por:
Já analisando a desigualdade da direita encontramos mais uma restrição para :
Logo, temos uma região acima da parábola, porém abaixo do eixo . Juntando essas duas condições, encontramos:
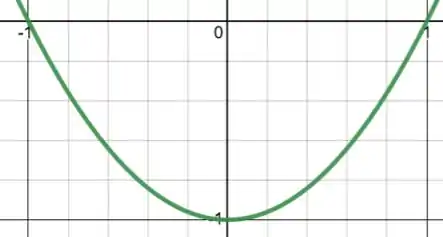
Muito bom!!
Passo 3
Agora precisamos calcular a área dessa região. Vamos usar aquilo que comentamos no passo :
Nesse caso, a região é limitada superiormente por:
E, inferiormente, por:
As intersecções e são dadas por:
Logo, montamos a integral:
Portanto:
Prontinho pessoal! Até a próxima 😊